Project Helena TBS/RPG (alpha version)

[eugeneloza]

http://sourceforge.net/projects/projecthelena/

Project Helena is a Win/Linux turn-based strategy/RPG game (at this point it is more of a strategy than a RPG). Player has several units and has to destroy enemy bots.
The turn-based battle system is similar to first X-coms, Jagged Alliance, Lost colony, etc.

The game is written completely in Lazarus/FPC, free and opensource .

Screenshot of the battle

What is ready: The game is a completely playable turn-based strategy. The player can select map parameters, difficulty and battle enemy bots. The game has 29 randomly-generated map types, good strategy for enemy bots.
ToDo: Still no sound & bad graphic. I'm going to switch to the Castle Game Engine for nice graphics and sound implementation. There's still almost no RPG part of the game. Also a tutorial will be implemented and controls will be made more WYSIWYG.

[Julius]

This is a cool project it seems. Not sure though if a switch to the CGE would make a lot of sense if it includes the need for 3D graphics which are considerably more difficult to create and source (but this might be a good start: http://opengameart.org/content/3rd-pers ... ci-fi-pack ).

Do you plan to include some sort of meta-game like the XCom base-management or something like that?

[eugeneloza]

considerably more difficult to create

As far as I tried - 3D graphics is much more simple for me than 2D. Still working to learn Blender, but I can already make some simple models like tanks or heads. And I don't think it will be too difficult to texture them with processed photos or other generated images. On the other hand, I can't draw at all Even the simplest sprites.

I need CGE for a much more complex project - Decoherence (a plot-based RPG). Therefore, I think, that I first try it on a 'simple' Project Helena, where there will be no 'humanoid' models, just cars and tanks, maybe some walking robots.

Do you plan to include some sort of meta-game like the XCom base-management or something like that?

While the there will be a RPG story (though it will not be complex), the main aspect of the game will be TBS.
The thing 'slowing me down' in this is graphic engine. I need to create windows with information/dialogue/shop/etc. At this moment I use TCanvas and it is AWFULLY SLOW. Moreover TCanvas cannot operate in a thread, i.e. no 'idle' animation is possible e.g. for smoke. On an old computer (1.2GHz) it takes up to 4 seconds to draw a complex map (with lots of smoke). And pure Lazarus has no decent cross-platform audio system (I tried several - they work either with alsa, either with pulseaudio, either with windows mixer, but never 'all of them together'). While CGE has both I plan to do everything for RPG part when I switch to this game engine.
Moreover CGE is cross-compilable to Android, which is another good advantage.

I've thought of some additional mechanics for Project Helena - a pure 'base vs base' strategy, to include base construction and even PvP mode (the game mechanics is suitable for this). But I don't know if that would be really demanded.

[eugeneloza]

Hi all!
The Project Helena is slowly moving to its Betta...
At this point the computer strategy has been significantly improved. So at this point I need more statistical data on battles outcome to make a good map difficulty estimate. I've added a battle log generator to the last version, and I would be very thankful if anybody could send me the logs (wins/looses) at different difficulties by e-mail in the program or in any other convenient way.
It would be very good if those would be not only wins, but also looses (so in case of something goes wrong at the very beginning of the battle, try to finish it anyway).

[Akien]

Awesome! I just gave it a try and it's quite fun :-)
I will send you a compilation of battle logs when I have played some more games.

You might want to add to the readme.txt file that the 32bit GTK+2 lib is necessary to run the game.
And maybe add an install.txt file with compilation instructions in the source distribution (currently there is only the readme which says "you don't have to compile anyting" ;-)).

[eugeneloza]

You might want to add to the readme.txt file that the 32bit GTK+2 lib is necessary to run the game.
And maybe add an install.txt file with compilation instructions in the source distribution (currently there is only the readme which says "you don't have to compile anyting" ;-)).

Oh... thanks... I didn't know about that ... I'll try to fix this asap.
It's compilied under Lazarus, requiring nothing additional... I'll try to figure out how to formulate it

[Akien]

It's compilied under Lazarus, requiring nothing additional... I'll try to figure out how to formulate it

I think there's a command-line instruction to build lazarus projects without having to load it all in the IDE, I think that would be the best.

Ah yes just found it out again, it's call lazbuild: http://wiki.lazarus.freepascal.org/lazbuild

[eugeneloza]

Test Snapshot of Project Helena


Castle Game Engine.
- Sound
- Music
- Graphics

Upgrade unfinished yet but already significantly improved.
Sorry for huge file size, but I haven't yet managed to involve libvorbis and the music is temporarily in WAV. I hope I'll fix it soon.

Win64bit. http://sourceforge.net/projects/project ... p/download
I'll try to recompile it for 32 bit and Linux soon.
All the required dll are provided. But in case no sound, OpenAL should be installed (available in the archive)

Stil missing:
Highlighting possible attack positions (really needed).
Shot animation
Damage display after explosion (already in place after usual shot).
Interface sometimes lags update (non critical).
And etc. according to 'todo' including improving music, sound & graphic.

[Danimal]

I tried it and it was pretty solid, i enjoyed the match even if it was unfair to me. It will be pretty nice once you add base/strategic components

[eugeneloza]

New testing version:
Win32 http://sourceforge.net/projects/project ... p/download
Linux32 http://sourceforge.net/projects/project ... z/download
Source http://sourceforge.net/projects/project ... z/download

New map tiles
New enemy bot type
Many bugfixes & visual improvements
Music is now in OGG (size reduced) & more sounds

i enjoyed the match even if it was unfair to me.

Yes... I know, I must make a tutorial, including some strategical hints I hope, It'll be ready in the nearest future, but not too soon.
Howver, a video tutorial might do a good job also until interacive in-game help&tutorial works. I'll try to record it soon, maybe even at these weekends.

It will be pretty nice once you add base/strategic components

Hmm... actually I didn't plan to add base components (only static shops, repair docks, etc.)
However, if this feature is required, I can make something like that. Will require much work thou (at the moment AI is RPG-ish (i.e. tactical + each computer bot behaves independently), not strategical).
The main developement accent now is RPG roadmap (events, quests, etc.)

[Vandar]

You said it is easier for you to model in 3D than to draw 2D sprites. It's a bit similar for me, but I just render the models and use the images as sprites in a 2D engine. That makes coding significant easier, at least for me.

This project looks very intersting to me. I was a huge fan of rthe early Battle Isle games, and your project shares the same basic principles.

[eugeneloza]

You said it is easier for you to model in 3D than to draw 2D sprites.

Yes... but I still can't make 3D part of the engine work...
So, had to pixelart something here, to fill the blank space Because rendered 3D will be too unsharp for such small tiles (20x20 px).
Low quality... but better than nothing.

It's a bit similar for me, but I just render the models and use the images as sprites in a 2D engine. That makes coding significant easier, at least for me.

Maybe, I'll do the same... however, not sure yet... I need 3D for the next very complex project, and it'll be a good experience.

[Vandar]

3D adds a new layer of complexity. There are more complex intersection and collision tests, animation, and soon there is a wish to move away from grid-based data structures towards something with free positions, which adds complexity again. I've often been wondering why the industry hyped the 3D so much, since most of the time, it doesn't add much to the actual gameplay.

[eugeneloza]

Highlighting ready More music from OGA. Now it's almost the stable version.
Win32 http://sourceforge.net/projects/project ... p/download
Source http://sourceforge.net/projects/project ... p/download

[Danimal]

will you upgrade the graphics to bigger ones? skorpio did some really nice sprites before

http://opengameart.org/content/space-sh ... tion-kit-2

[eugeneloza]

will you upgrade the graphics to bigger ones? skorpio did some really nice sprites before

Thanks, but 2D is an intermediate results (to learn Castle Game Engine better). As soon as I understand how to access TShape from TX3DrootNode I'll start making it 3D.
P.S. The Scorpio's sprites are really cool!!!

[eugeneloza]

Almost a stable version:
Item description is back in Testing
Russian is back in Testing
Caution mode is back in Testing
(+) Time Units remaining are displayed in Caution mode plus time to recharge also displayed

Still some optimizations & bugfixes needed...

Win32 http://sourceforge.net/projects/project ... p/download
source http://sourceforge.net/projects/project ... p/download

[eugeneloza]

Last testing step before the 'stable' branch If everything works, then that's it

(Many bugfixes and minor imrpvements)
(upd: a small bugfix)
Win32 http://sourceforge.net/projects/project ... p/download
Source http://sourceforge.net/projects/project ... p/download

I'd be very grateful if you could ping me that everything works. And if any errors show up, please, write me.

[Danimal]

i had my ass handed down to me again , so far no crashes or errors happened to me. New music is nice, it could use a bit more explanation about items, i just pick them up but dont really know the difference between weapons

[eugeneloza]

Thanks a lot for the feedback!
I'll try to make the video tutorial till Monday Now, the only explanation is DOC/ProjectHelenaHelp.pdf. It explains all aspects of game mechanics, but in text format... Finally, I'll make an interactive tutorial... but for now video tutorial will be much better.

[eugeneloza]

Back to stable branch: http://sourceforge.net/projects/projecthelena/

Seemed so obvious to me, but I took me 14 minutes to explain all the controls... I must seriously optimize the interface!

Video Tutorial is ready:
English

youtu.be/IgBMOA3ALT8
Russian
http://www.youtube.com/watch?v=0_imyKhhD_U

[eugeneloza]

Made a 'Let's play' video : An epic fail at 150th difficulty.

Part1

youtu.be/Nh38Gme59-Q

Part2

youtu.be/kfc-QtcCpmU

[eugeneloza]

Finally (thanks to Akien for reminding me) I've moved to GitHub repositorium. https://github.com/eugeneloza/Project-Helena

And an epic victory at difficulty level 166 with annotations.

youtu.be/jxaf9ku6l2Q

youtu.be/wTq9fYAslfs

[eugeneloza]

Eventually I've finished Monte-Carlo difficulty estimate for Project Helena.

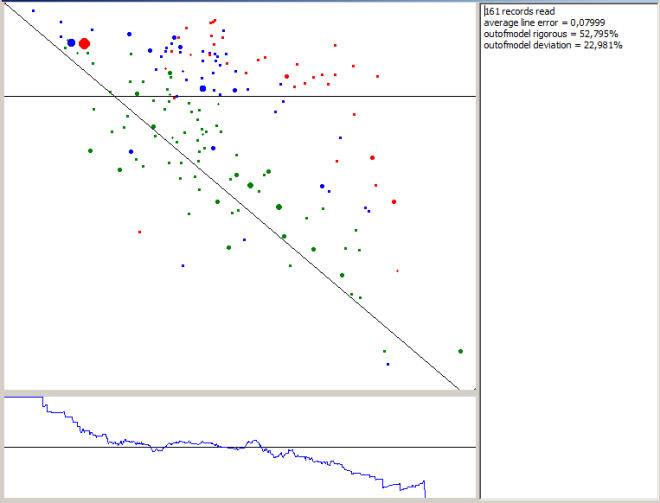
Points on graph: real results of 161 battles. Green - good concordance of model results with real results, blue - average, and red - bad concordance.
Vertical axis is battle result (horizontal black line is "0": above - victory, below - defeat), horizontal axis - battle results calculated by Monte-Carlo. Oblique black line is 1:1.
Lower graph is empiric victory chance, black line - 50%.

The Monte-Carlo algorithm input is:
N and HP of enemy
N and HP of player
A few generalized map properties (area, %free area, average tiles visible from a map tile)

The method models the following:
a local battle of player against a few bots.
Chance of player ammo shortage & ammo collection
Chance of another enemy bots enter the local battle

What IS NOT modeled:
Successful hiding.
Successful use of bottlenecks.
Bazookas.

Based on ~10000 model battles I get
botstogether - how many bots attack the player together
bestscore,worstscore - best and worst score
averagegoodscore,averagebadscore - average good and bad scores
averagescore - average score
scoredeviation - average dispersion
outofammochance - Chance that at least once the player will feel ammo shortage.
victorychance - victory chance
battleturns - a very good lower estimate of battle length

Well... 53% empiric results are outside averagegoodscore...averagebadscore
E.g. the "last to the right victory" ended up in score 21%, while calculations give Average score: -238,73% Best score: 27,5% Average good score: -174,71% Average bad score: -262,82% Worst score: -313% Victory chance: 0,04%

Hard to say what to do

There is a possibility to model a real battle, based on real bots characteristics and locations, real properties of their weapons. However, that result might be also inadequate. Moreover, such modeling will take much more computational time (and I have no statistics to backward-calculate a decent amount of empiric data).

[eugeneloza]

Even more epic victory - beating 187% difficulty recorded!

youtu.be/y1rhl3HtfPo

youtu.be/VrIQ0TXWZ6A

And and unexpected revelation in difficulty estimate:

I can clearly see two "branches" - regular and well-modeled defeats when the player is ovewhelmed by enemy bots and out-of-model victories in case the player takes advantages of map peculiarities and enemy distribution on the map is rather even. Well... it remains only to come up with a good algorithm describing the second branch!